Month: Հոկտեմբեր 2024

1)AD մեծ հիմքով ABCD սեղանի AC անկյունագիծը ուղղահայաց է CD սրունքին, <BAC = <CAD։ Գտեք AD-ն, եթե սեղանի պարագիծը 20 սմ է, իսկ <D = 60^o։

P=20

x+x+x+2x=20

5x=20

x=20:5=4

4×2=8

2)M և N կետերը գտնվում են տրված ուղղի մի կողմում, և նրանց հեռավորությունները այդ ուղղից հավասար են 10սմ և 22սմ։ Գտեք MN հատվածի միջնակետի հեռավորությունը այդ ուղղից։

10+22=32

32:2=16

3)Ուղղանկյուն սեղանի մեջ սուր անկյունը 45^o է։ Փոքր սրունքը և փոքր հիմքը 10-ական սմ են։ Գտեք սեղանի մեծ հիմքը։

20

Լրացուցիչ աշխատանք (տանը).

1)Տրված է BE II CD, գտնել <ABC,<C,<D:

180-40=140

180-140-75=65

180-65=115

180-115=65

180-65=115

2)Ըստ գծագրի տվյալների հաշվել AD կողմը։

20

1)Հավասարասրուն սեղանի սրունքը հավասար է փոքր հիմքին և մեծ հիմքից փոքր է 2 անգամ։ Գտե՛ք սեղանի պարագիծը, եթե փոքր հիմքը 7սմ է։

7×2=14

14+7+7+7=35

2)ABCD հավասարասրուն սեղանի C գագաթից AD մեծ հիմքին տարված է CK ուղղահայացը։ Գտե՛ք սեղանի հիմքերը, եթե դրանց գումարը 18սմ է, իսկ KD=1սմ։

8սմ

10սմ

3)Հավասարասրուն սեղանի անկյունագիծը կիսում է դրա բութ անկյունը։ Սեղանի փոքր հիմքը 3սմ է, իսկ պարագիծը՝ 42սմ։ Գտե՛ք սեղանի մեծ հիմքը։

42-3=39

39:3=13

Լրացուցիչ աշխատանք (տանը).

1)Գտե՛ք 13սմ և 19սմ հիմքերով սեղանի միջին գիծը։

13+19=32

32:2=16

2)Հավասարասրուն սեղանի մեծ հիմքը երկու անգամ մեծ է փոքր հիմքից։Սեղանի անկյունագիծը դրա սուր անկյունը բաժանում է հավասար մասերի։ Գտե՛ք սեղանի փոքր հիմքը, եթե սեղանի պարագիծը 60սմ է։

60:5=12

12×2=24

3)Գտե՛ք սեղանի հիմքերի երկարությունները, եթե դրանց տարբերությունը 7սմ է, իսկ սեղանի միջին գիծը 12սմ է։

12×2=24

x+x+7=24

24-7=17

17:2=8,5

8,5+7=15,5

1)Գտեք հավասարասրուն սեղանի անկյունները, եթե հայտնի է, որ սեղանի երկու անկյունների տարբերությունը 40^o  է։

110,70, 110, 70

2)Հավասարասրուն սեղանի մեծ հիմքը 4մ է, սրունքը՝ 2մ, իսկ դրանց կազմած անկյունը՝ 60^o ։ Գտեք սեղանի փոքր հիմքը։

2մ

3)Սեղանի հիմքերը հարաբերում են, ինչպես 2:3, իսկ միջին գիծը 10սմ է։ Գտեք սեղանի հիմքերը։

10×2=20

4×2=8

4×3=12

Լրացուցիչ աշխատանք (տանը).

1)Գտեք AD և BC հիմքերով սեղանի B և D անկյունները, եթե < A = 36^o, < C = 117^o։

<B=180-36=144

<D=180-117=63

2)Հավասարասրուն սեղանի բութ անկյան գագաթից նրա մեծ հիմքին տարված ուղղահայացն այդ հիմքը տրոհում է 6սմ և 30սմ երկարությամբ հատվածների։ Գտեք սեղանի փոքր հիմքը և միջին գիծը։

36+24=60

60:2=30

Սեղան է կոչվում այն քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը զուգահեռ չեն:

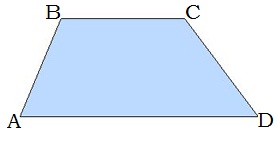
Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր:

AD -ն և BC -ն սեղանի հիմքերն են:  

Սեղանի կողմերը, որոնք զուգահեռ չեն, կոչվում են սրունքներ:

AB -ն և CD -ն սեղանի սրունքներն են:  

Սեղանի հատկությունները․

Սեղանի ներքին անկյունների գումարը (ցանկացած քառանկյան) 360° է:

Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:

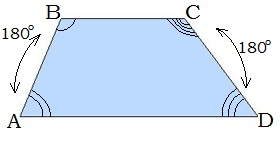
Կան սեղանի մի քանի տեսակներ: Հաճախ դիտարկվում են ուղղանկյուն և հավասարասրուն սեղանները:

Ուղղանկյուն սեղան

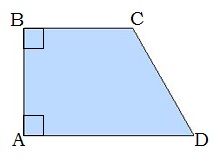
Սեղանը կոչվում է ուղղանկյուն սեղան, եթե նրա սրունքներից որևէ մեկը ուղղահայաց է հիմքերին:

Հավասարասրուն սեղան

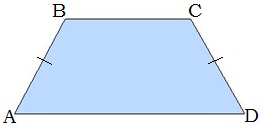
Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան:

Հետևյալ հատկությունները բնորոշ են միայն հավասարասրուն սեղաններին:

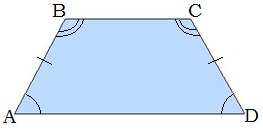
1. Հավասարասրուն սեղանի հիմքերին առընթեր անկյունները զույգ առ զույգ հավասար են:

2. Հավասարասրուն սեղանի անկյունագծերը հավասար են:

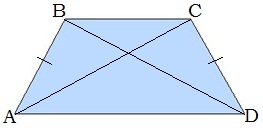
AC=BD

Հավասարասրուն սեղանի հայտանիշները․

1. Եթե սեղանի հիմքին առընթեր անկյունները հավասար են, ապա սեղանը հավասարասրուն է:

2. Եթե սեղանի անկյունագծերը հավասար են, ապա սեղանը հավասարասրուն է:

Սեղանի միջին գիծը․

Սեղանի սրունքների միջնակետերը միացնող հատվածը կոչվում է սեղանի միջին գիծ:

Սեղանի միջին գիծը զուգահեռ է հիմքերին և հավասար է նրանց կիսագումարին:

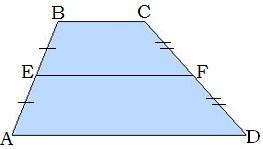
EF∥BC

EF∥AD

EF=(BC+AD)/2

Սեղանն ունի ընդամենը մեկ միջին գիծ:

Առաջադրանքներ․

1) Տրված է՝ ∢A=37°∢C=121° : Գտիր՝ ∢B,∢D-ն։

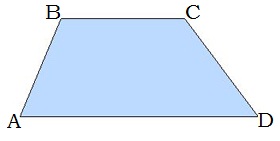
180-37=143

180-121=59

2)Հաշվիր ABCD սեղանի անկյունները, եթե ∢A=30°:

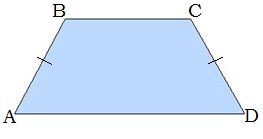
D=A=30

180-30=150

B=C=150

3) Տրված է՝ AE=EB, CF=FD, BC=28 մ, AD=30 մ: Գտիր՝ EF-ը:

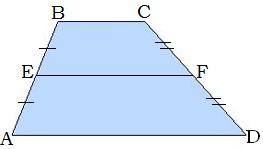
30+28=58

58:2=29

4)Սեղանի հիմքերի հարաբերությունը հավասար է 2:7: Հաշվիր սեղանի մեծ հիմքը, եթե նրա փոքր հիմքը հավասար է 12 սմ -ի:

12։2=6
6*7=42
Լրացուցիչ աշխատանք (տանը)․

1) Նշիր ճիշտ պնդումը՝

ա)Հավասարասրուն սեղանի սրունքները զուգահեռ են:

բ)Ուղղանկյուն սեղանի հիմքերը հավասար են:

գ)Ցանկացած սեղանի հիմքերը զուգահեռ են:

2)Սեղան կոչվում է այն քառանկյունը, որի

ա)կողմերը զույգ առ զույգ զուգահեռ են:

բ)երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը՝ ոչ:

3) Սեղանը կոչվում է հավասարասրուն, եթե

ա)նրա սրունքները հավասար են:

բ)նրա սրունքները զուգահեռ են:

Տեսական մասը կրկնեք այստեղ․

Առաջադրանքներ․

1)Զուգահեռագծի պարագիծը 48սմ է։ Գտեք զուգահեռագծի կողմերը, եթե՝

ա) կողմերից մեկը մյուսից մեծ է 3 սմ-ով,

x+x+3+x+x+3=48
4x+6=48
4x=48-6
4x=42
x=42/4
x=10,5
10,5+3=13,5

բ) կողմերից մեկը երկու անգամ մեծ է մյուսից:

x+2x+x+2x=48
6x=48
x=48/6
x=8
8×2=16

գ)կողմերից մեկը երկու անգամ մեծ է մյուսից
1+3=4
48:4=12 (1)
12*3=36 (3)

2)Ըստ գծագրի տվյալների՝ գտե՛ք զուգահեռագծի պարագիծը.

3x+5=6x-10

x=20

DA=15

15+15+20+20=70

3)ABCD զուգահեռագծի պարագիծը 50 սմ է, <C=30⁰, իսկ CD ուղղին տարված BH ուղղահայացը 6,5 սմ է։ Գտեք զուգահեռագծի կողմերը։

Լրացուցիչ աշխատանք (տանը).

1)Գտե՛ք ABCD զուգահեռագծի անկյունները, եթե՝

ա) ∠ A = 45°
45×2=90

180-90=90

90:2=45

բ) ∠ C – ∠ D = 50°

գ) ∠ A + ∠ C = 81°
180-81=99

99:2=49,5

դ) ∠ A = 0,5∠ B։

2)Ըստ գծագրի տվյալների՝ գտե՛ք զուգահեռագծի պարագիծը.

3)Զուգահեռագծի կիսապարագիծը 24 սմ է, կողմերից մեկը երկու անգամ մեծ է մյուսից, իսկ մեծ կողմին տարված բարձրությունը 4 սմ է։ Գտե՛ք զուգահեռագծի անկյունները։

Զուգահեռագիծ կոչվում է այն քառանկյունը, որի հանդիպակաց կողմերը զույգ առ զույգ զուգահեռ են:

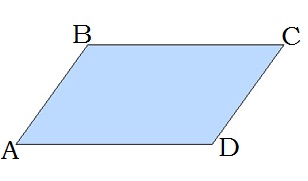
Զուգահեռագծի հատկությունները.

1. Զուգահեռագծի հանդիպակաց կողմերը հավասար են՝ AB=DC,BC=AD

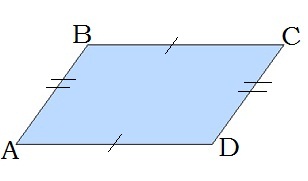
2. Զուգահեռագծի հանդիպակաց անկյունները հավասար են՝ ∢A=∢C,∢B=∢D

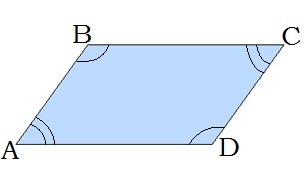
3. Զուգահեռագծի անկյունագծերը հատման կետով կիսվում են՝ BO=OD, AO=OC

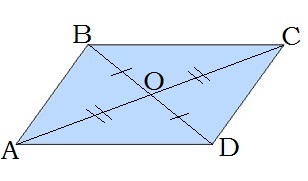
4. Զուգահեռագիծը անկյունագծով բաժանվում է երկու հավասար եռանկյունների՝ ABC և CDA եռանկյունները հավասար են:

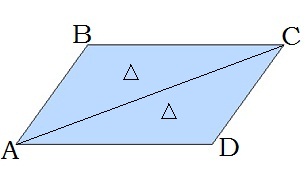
5. Զուգահեռագծի յուրաքանչյուր կողմին առընթեր անկյունների գումարը 180 աստիճան է՝ ∢A+∢D=180°

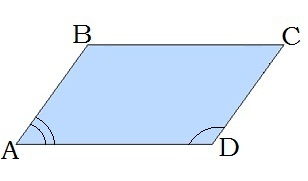
6. Անկյունագծի խաչադիր անկյունները հավասար են՝ ∢BAC=∢ACD, ∢BCA=∢CAD

Զուգահեռագծի հայտանիշները.

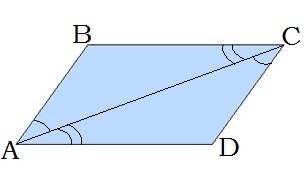
Զուգահեռագծի հայտանիշները թույլ են տալիս պարզելու, թե արդյո՞ք տրված քառանկյունը զուգահեռագիծ է:

1. Եթե քառանկյան երկու կողմերը հավասար են և զուգահեռ, ապա քառանկյունը զուգահեռագիծ է: 

2. Եթե քառանկյան հանդիպակաց կողմերը զույգ առ զույգ հավասար են, ապա քառանկյունը զուգահեռագիծ է: 

3. Եթե քառանկյան անկյունագծերը հատվում և հատման կետով կիսվում են, ապա քառանկյունը զուգահեռագիծ է:

Առաջադրանքներ․

1)

P=6+6+10+10=32

2)

3)

AB = 15

AD = 30

Լրացուցիչ աշխատանք (տանը).

1)

Հիմա բացատրեմ ինչու ՝ եթե A-ն 40 աստիճան է ապա C-ն էլ, քանի որ զուգահեռագծի հանդիպակաց անկյունները հավասար են՝ ∢A=∢C,∢B=∢D, իսկ B-ն հավասար է 140 , քանի որ զուգահեռագծի յուրաքանչյուր կողմին առընթեր անկյունների գումարը 180 աստիճան է՝ ∢A+∢B=180° իսկ 180 — 40 = 140, իսկ եթե B-ն 140 է ապա D-ն էլ է 140

2)

A անկյունը՝ 60

B անկյունը՝ 120

3)

BO = 6

OC = 8,5

Դիցուք տրված է x և y անհայտներով գծային հավասարումների համակարգ՝

{a₁x+b₁y+c₁=0

{a₂x+b₂y+c₂=0

(x;y) թվազույգը կոչվում է համակարգի լուծում, եթե այն բավարարում է համակարգի հավասարումներից յուրաքանչյուրին:

Առաջին աստիճանի գծային հավասարմանը բավարարում են նրա գրաֆիկի՝ ուղիղ գծի վրա գտնվող բոլոր (x;y) կետերը:

Հետևաբար, եթե մենք ուզում ենք, որ բավարարվեն համակարգի երկու գծային հավասարումները միաժամանակ, ուրեմն պետք է փնտրել այնպիսի (x;y) կետեր, որոնք միաժամանակ պատկանում են երկու ուղիղներից յուրաքանչյուրին:

Այսպիսով, համակարգի լուծումները համակարգի հավասարումներով տրվող ուղիղների (գրաֆիկների) ընդհանուր կետերն են:

Օրինակ՝

1. Լուծենք հետևյալ համակարգը:

{x+2y−5=0,

{2x+4y+3=0

x+2y−5=0 հավասարման գրաֆիկն ուղիղ գիծ է: Կառուցենք այդ ուղիղը:  

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	5	0
y	0	2,5

xОy հարթության վրա կառուցենք գտնված (5;0) և (0;2.5) կետերը և դրանցով տանենք l1 ուղիղը:

2x+4y+3=0 հավասարման գրաֆիկը ևս ուղիղ գիծ է: 

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	−1,5	2,5
y	0	−2

xОy հարթության վրա կառուցենք գտնված (−1.5;0) և (2.5;−2) կետերը և դրանցով տանենք l2 ուղիղը:

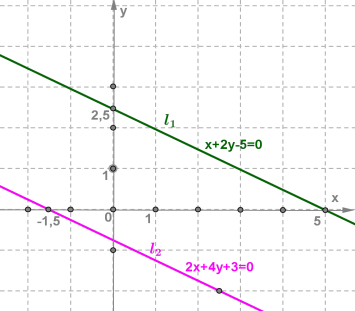
l1 և l2 ուղիղները զուգահեռ են և չունեն ընդհանուր կետեր:

Պատասխան՝ համակարգը լուծում չունի:   

Օրինակ՝

2. Լուծենք հետևյալ համակարգը:

{2x−y−5=0,

{2x+y−7=0

Համակարգի հավասարումները բերենք գծային ֆունկցիայի ընդհանուր տեսքին՝ y=2x−5 և y=−2x+7

y=2x−5 ֆունկցիայի գրաֆիկը ուղիղ գիծ է:

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	0	3
y	−5	1

xОy հարթության վրա կառուցենք գտնված (0;−5) և (3;1) կետերը և դրանցով տանենք l1 ուղիղը:

y=−2x+7 ֆունկցիայի գրաֆիկը ուղիղ գիծ է:

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	0	1
y	7	5

xОy հարթության վրա կառուցենք գտնված (0;7) և (1;5) կետերը և դրանցով տանենք l2 ուղիղը:

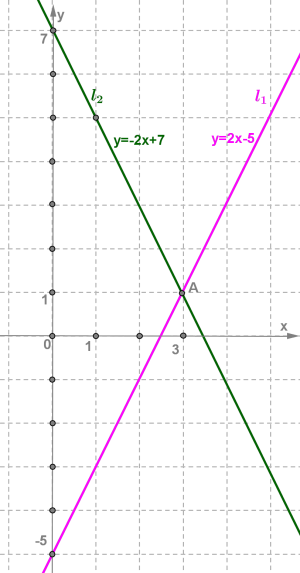
l1 և l2 ուղիղները հատվում են A կետում, որի կոորդինատները համակարգի միակ լուծումն են:

Պատասխան՝ (3;1)

Օրինակներում կիրառեցինք համակարգերի լուծման գրաֆիկական եղանակը:

Գրաֆիկական եղանակը հուսալի չէ, քանի որ միշտ չի հաջողվում ճշգրիտ գտնել հատման կետի կոորդինատները: Այդ պատճառով, խորհուրդ է տրվում գրաֆիկորեն գտնված կետը տեղադրել համակարգի հավասարումների մեջ և համոզվել, որ դրանք բավարարվում են:

Այսպիսով, գալիս ենք հետևյալ եզրակացություններին:

1. Համակարգի հավասարումներով տրված ուղիղները կարող են հատվել մեկ կետում: Այդ կետի կոորդինատները համակարգի միակ լուծումն են:

2. Համակարգի հավասարումներով տրված ուղիղները կարող են լինել զուգահեռ և չհատվել: Այս դեպքում համակարգը լուծում չունի:

3. Համակարգի հավասարումներով տրված ուղիղները կարող են համընկնել: Այս դեպքում համակարգն ունի անվերջ թվով լուծումներ:

Առաջադրանքներ․

Հավասարումների համակարգը լուծել գրաֆիկական եղանակով․

1)

2;0
2)

Լուծում չունի :

3)

Պատ. 3;1

4)

Հատման կետը ՝ 0;1

անվերջ լուծումներ:

Օրինակ (հնագույն) Հանդիպեցին երկու հովիվ՝ Հովհաննեսը և Պետրոսը: Հովհաննեսն ասում է Պետրոսին. «Տուր ինձ մի ոչխար, և ինձ մոտ կլինի երկու անգամ ավելի ոչխար, քան քեզ մոտ»: Իսկ Պետրոսը նրան պատասխանում է. «Ոչ, ավելի լավ է դու տուր ինձ մի ոչխար, և մեզ մոտ կլինեն հավասար թվով ոչխարներ»: Քանի՞ ոչխար ուներ նրանցից յուրաքանչյուրը:

Լուծում: Դիցուք Հովհաննեսն ուներ x ոչխար, իսկ Պետրոսը՝ y ոչխար: Եթե Պետրոսը Հովհաննեսին տար մեկ ոչխար, ապա Պետրոսի մոտ կմնար (y-1) ոչխար, իսկ Հովհաննեսի մոտ կլիներ (x+1) ոչխար:

Բայց այդ դեպքում Հովհաննեսի մոտ երկու անգամ շատ ոչխար կլիներ, քան Պետրոսի մոտ: Հետևաբար

                                        x+1=2(y-1):

Իսկ եթե Հովհաննեսը Պետրոսին մեկ ոչխար տար, ապա Հովհաննեսի մոտ կմնար (x-1) ոչխար, իսկ Պետրոսի մոտ կդառնար (y+1) ոչխար: Բայց այդ դեպքում նրանք կունենային հավասար թվով ոչխարներ: Հետևաբար

                                      x-1=y+1:

Այս երկու հավասարումներից կազմենք համակարգ՝

Համակարգն էլ լուծելով մեզ արդեն ծանոթ տեղադրման կամ գումարման եղանակով՝ կստանանք, որ x=7; y=5: Այսպիսով, Հովհաննեսն ունի 7 ոչխար, իսկ Պետրոսը՝ 5 ոչխար:

Առաջադրանքներ․

1) 

ա) Երկու թվերի գումարը 10 է, իսկ տարբերությունը՝ 4: Գտեք այդ թվերը:
7; 3

բ) Երկու թվերի գումարը 21 է, իսկ տարբերությունը՝ 9: Գտեք այդ թվերը:
15; 6

2) Մի թիվը 2 անգամ մեծ է մյուսից: Եթե այդ թվերից փոքրը մեծացվի 4 անգամ, իսկ մեծը՝ 2 անգամ, ապա նրանց գումարը հավասար կլինի 44: Գտեք այդ թվերը:
11; 5

3) Տրված են երկու թվեր։ Եթե առաջին թիվը բազմապատկենք 2-ով, ապա ստացված թիվը 1-ով մեծ կլինի երկրորդից, իսկ եթե երկրորդ թիվը բազմապատկենք 2-ով, ապա ստացված թիվը 7-ով մեծ կլինի առաջինից։ Գտեք այդ թվերը։
3; 5

Լրացուցիչ աշխատանք (տանը)․

1)

 ա) Մի թիվը 6-ով մեծ է մյուսից: Այդ թվերի գումարը հավասար է 40-ի: Գտեք այդ թվերը:
17; 23

բ) Մի թիվը 15-ով փոքր է մյուսից: Գտեք այդ թվերը, եթե նրանց գումարը 23 է:
19; 4

2) Մի թիվը 7-ով մեծ է մյուսից: Եթե փոքր թիվը մեծացվի 2 անգամ, իսկ մեծը՝ 6 անգամ, ապա նրանց գումարը կդառնա 31: Գտեք այդ թվերը:
— 8/11; 45/8

3)Լուծիր համակարգը քեզ հարմար եղանակով։

7; 2

1; 5