Տարածական պատկերներ։ Զուգահեռանիստի սահմանումն ու հատկությունները

Երկրաչափության այն բաժինը, որը ուսումնասիրում է պատկերների հատկությունները տարածության մեջ, կոչվում է տարածաչափություն: Այն պատկերը, որի ոչ բոլոր կետերն են ընկած միևնույն հարթության մեջ, կոչվում է տարածական պատկեր:

Զուգահեռանիստի սահմանումն ու հատկությունները.

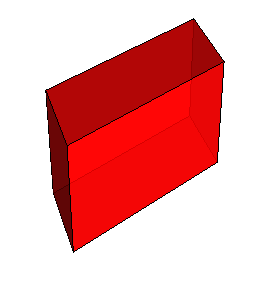
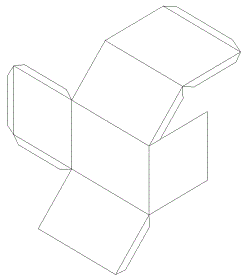
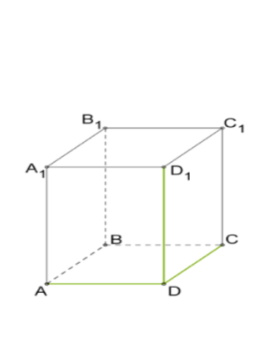
Զուգահեռանիստ  կոչվում է այն բազմանիսը, որի բոլոր 6 նիստերը զուգահեռագծեր են:

Բազմանկյունները, որոնցից կազմված է բազմանիստի մակերևույթը, կոչվում են նիստեր: Նիստերի կողմերը կոչվում են բազմանիստի կողեր: Կողերի ծայրակետերը կոչվում են բազմանիստի գագաթներ:

Զուգահեռանիստն ունի 6 նիստ, 8 գագաթ և 12 կող:

Զուգահեռանիստի ընդհանուր կող ունեցող նիստերը կոչվում են կից, իսկ ընդհանուր կողեր չունեցող նիստերը՝ հանդիպակաց:

Զուգահեռանիստի հիմքեր անվանում են նրա որևէ երկու հանդիպակաց նիստերը, իսկ մնացած նիստերը՝ կողմնային նիստեր: 

Հիմքերին չպատկանող կողերը կոչվում են զուգահեռանիստի կողմնային կողեր: 

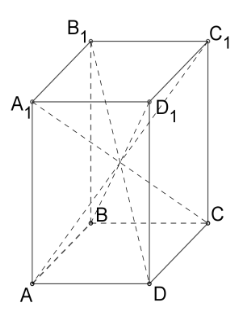
Նույն նիստում չգտնվող երկու գագաթները միացնող հատվածը կոչվում է զուգահեռագծի անկյունագիծ: 

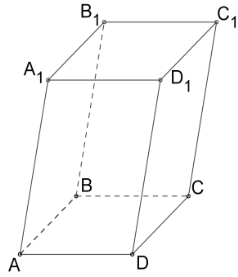
Գոյություն ունեն զուգահեռանիստերի երկու տեսակ՝

— ուղիղ,

— թեք:

Ուղիղ զուգահեռանիստերի կողմնային նիստերը ուղղանկյուններ են:

Թեք զուգահեռանիստի կողմնային նիստերը զուգահեռագծեր են:

Ուղիղ զուգահեռանիստը, որի հիմքերը ևս ուղղանկյուններ են, կոչվում է ուղղանկյունանիստ:

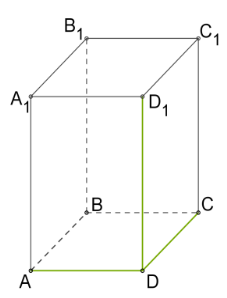
Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

Զուգահեռանիստի հատկությունները:

— Զուգահեռանիստի հանդիպակաց նիստերը զուգահեռ են և հավասար:

— Զուգահեռանիստի բոլոր չորս անկյունագծերը հատվում են միևնույն կետում և այդ կետում կիսվում են: 

— Ուղիղ զուգահեռանիստերի կողմնային նիստերը ուղղանկյուններ են: 

Առաջադրանքներ․

1)

ա)

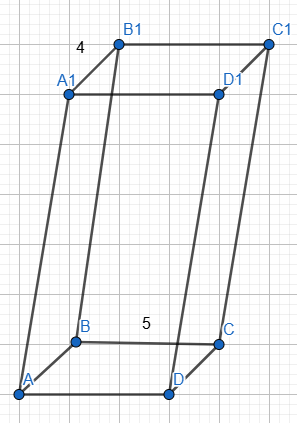
BC=B1C1=5
A1B1=AB=4
AB=DC=4
բ)

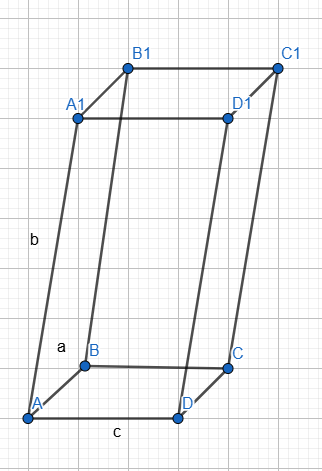
AD=BC=c
A1A=C1C=b
BA=CD=a

2)

48:12=4

3)

32:4=8
8*12=96