Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ

Եթե քառանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ քառանկյան ներգծյալ շրջանագիծ:

Ոչ բոլոր քառանկյուններն ունեն ներգծյալ շրջանագիծ, քանի որ՝ չորս անկյունների կիսորդները կարող են նույն կետում չհատվել: 

Եթե քառանկյանը ներգծվել է շրջանագիծ, ապա քառանկյան հանդիպակաց կողմերի գումարները հավասար են՝  a+c=b+d:

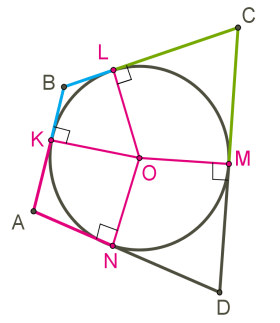
Եթե քառանկյան հանդիպակաց կողմերի գումարները հավասար են, ապա այդ քառանկյունն ունի ներգծյալ շրջանագիծ:

Եթե քառանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:

Ոչ բոլոր քառանկյունները ունեն արտագծյալ շրջանագիծ՝ հաճախ քառանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի քառանկյան բոլոր չորս գագաթներով: 

Այս հարցը պարզվում է հետևյալ պնդման միջոցով:

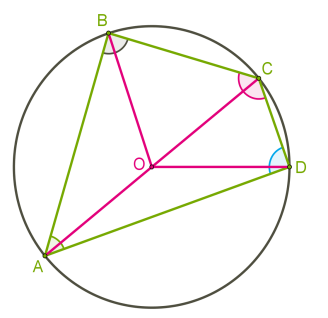
Եթե քառանկյան հանդիպակաց անկյունների գումարը 180° է, ապա նրան կարելի է արտագծել շրջանագիծ:

Առաջադրանքներ․

1)Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերը հավասար են 2սմ և 8սմ։ Գտեք սեղանի պարագիծը։

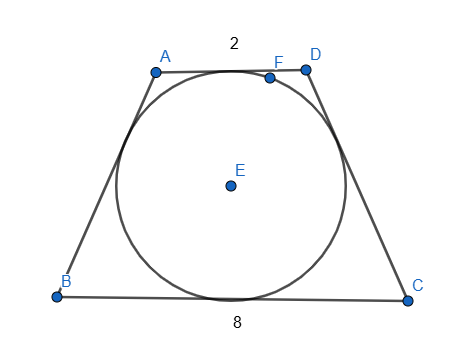
8+2=10
10+10=20

2)Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերից մեկը հավասար է մյուսի եռապատիկին, իսկ սեղանի սրունքը 8սմ է։ Գտեք սեղանի հիմքերը։

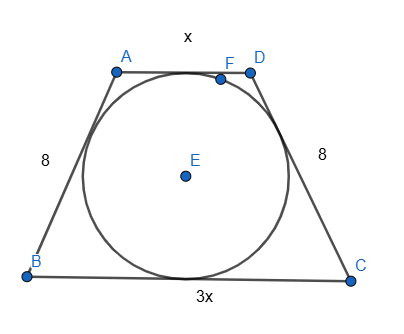
x+3x=8+8
4x=16
x=4

3)Գտեք շրջանագծին արտագծած հավասարասրուն սեղանի կողմերը, եթե նրա պարագիծը 40սմ է, իսկ հիմքերից մեկը 4 անգամ փոքր է մյուսից։

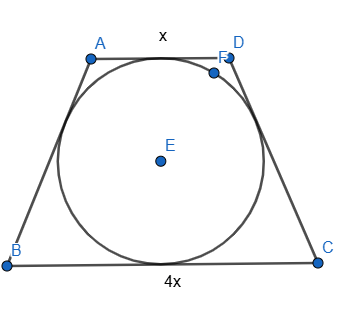
x+4x=y+y
5x=2y
x+4x+y+y=40
5x+2y=40
2y+2y=40
4y=40
y=10
5x=20
x=4
4•4=16

4)Հավասարասրուն սեղանին ներգծած է շրջանագիծ։ Այդ սեղանի պարագիծը 60սմ է։ Գտեք նրա սրունքը։

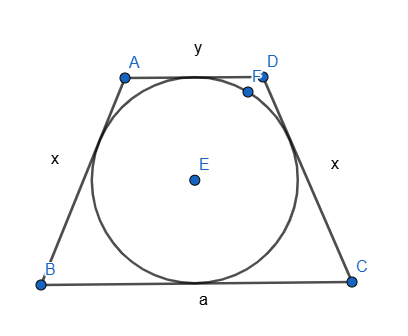
P=60
a+y=2x
P=a+y+2x
P=4x
60:4=15
x=15

5)Հավասարասրուն սեղանի սրունքը 8սմ է, իսկ փոքր հիմքին առընթեր անկյունների գումարը՝ 300^օ ։ Գտեք այդ սեղանին ներգծած շրջանագծի շառավիղը։

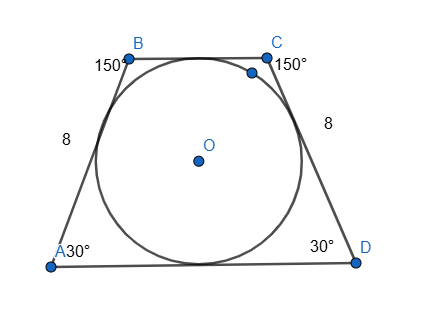
<B+<C=300
2r=8:2=4
r=4:2=2