Առաջին աստիճանի մեկ անհայտով անհավասարումներ

kx−b>0 կամ kx−b<0 տեսքի անհավասարումները, որտեղ k -ն և b -ն տրված թվեր են, ընդ որում k≠0, անվանում են առաջին աստիճանի մեկ x անհայտով անհավասարումներ:

Օրինակ․

a−5>0 a>5 Պատասխան՝a∈(5;+∞)

−2y−100<0 −2y<100|:(−2) (անհավասարության նշանը փոխվում է) y>100:(−2) y>−50 Պատասխան՝y∈(−50;+∞)

−3c≥−15|:(−3)(անհավասարության նշանը փոխվում է) c≤−15:(−3) c≤5 Պատասխան՝ c∈(−∞;5]

kx−b≥0 կամ  kx−b≤0 տեսքի անհավասարումները, որտեղ k -ն և b -ն տրված թվեր են, ընդ որում  k≠0, անվանում են մեկ  x անհայտով առաջին աստիճանի ոչ խիստ անհավասարումներ:

Օրինակ․

x−3≥0

x≥3

Պատասխան՝x∈[3;+∞)

Առաջադրանքներ․

1)Կոորդինատային առանցքի վրա պատկերեք միջակայքը՝

ա)(-2; 7)

բ)(-17; 34)

գ)(1234; 1398)

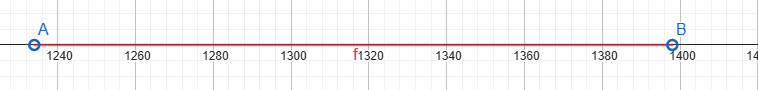
դ)(-∞; 0)

ե)(0; +∞)

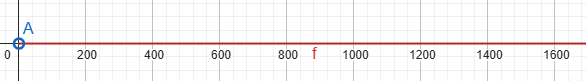
զ)(-∞; -3)

է)(2; +∞)

ը)(-∞; +∞)

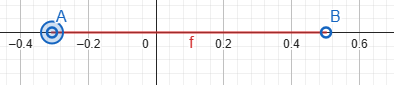
թ)(- 1/3; 0,5)

2)Ինչպիսի՞ նշան (<; =; >) պետք է դնել a և b թվերի միջև, եթե a-b տարբերությունը՝

ա)դրական թիվ է a>b

բ)բացասական թիվ է a<b

3)Նկարում պատկերված միջակայքերը գրեք անհավասարությունների նշանների օգնությամբ։

X>1 X ∈ (1;+∞)
X<0 X ∈ (-∞;0)
-1<X<3 X ∈ (-1;3)

4)Կոորդինատային առանցքի վրա պատկերեք բոլոր այն թվերը, որոնք բավարարում են նշված անհավասարումներին՝

ա)x > 0

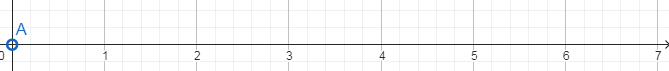
բ)x < 3

գ)x > 3579

դ)x < -2

ե)x > -1748

զ)x < 0,00006

5)x — a տարբերությունը համեմատեք զրոյի հետ, եթե

ա)x > a մեծ է զրոյից

բ)x < a փորք է զրոյից

6)3 թիվը հանդիսանո՞ւմ է նշված անհավասարման լուծում՝

ա)x > 0

∈ 

բ)x > -2

∈ 

գ)x < 3,1

∈ 

դ)-3 < x < 3

∉ 

ե)2,(8) < x < 3,1

∈