Category: Երկրաչափություն 8

Հարթության մեջ երկու շրջանագծերի փոխադարձ դասավորությունը կախված է՝

• նրանց կենտրոնների դասավորությունից, 
• նրանց շառավիղների երկարություններից: 

Հնարավոր է երեք դեպք:

1) Երկու շրջանագծերը հատվում են՝ ունեն երկու ընդհանուր կետ:

2) Երկու շրջանագծերը շոշափում են՝ ունեն մեկ ընդհանուր կետ:

3) Երկու շրջանագծերը ընդհանուր կետեր չունեն:

Դիտարկենք հնարավոր դեպքերը:

1) Երկու շրջանագծերը հատվում են. ունեն երկու ընդհանուր կետ:

Այս դեպքում կենտրոնների հեռավորությունը փոքր է շառավիղների գումարից:

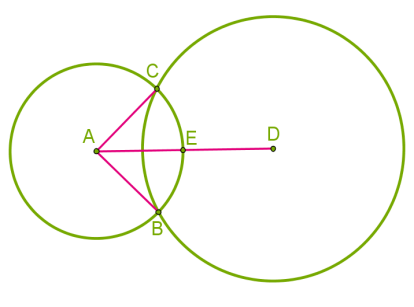
2) Երկու շրջանագծերը շոշափում են. ունեն մեկ ընդհանուր կետ:

Այս դեպքում հնարավոր են հետևյալ դեպքերը՝

• արտաքին շոշափում,
• ներքին շոշափում:

Արտաքին շոշափման ժամանակ կենտրոնների հեռավորությունը հավասար է շառավիղների գումարին:

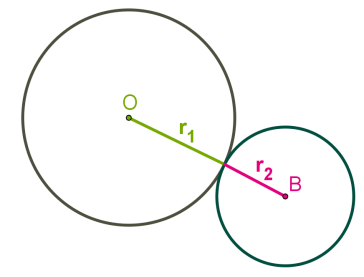
Ներքին շոշափման ժամանակ կենտրոնների հեռավորությունը հավասար է շառավիղների տարբերությանը:

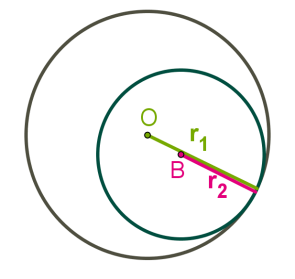
3) Երկու շրջանագծերը ընդհանուր կետեր չունեն:

Այս դեպքում ևս հնարավոր է երկու դեպք:

• Երկու շրջանագծերով սահմանափակված շրջանները չեն հատվում:
• Փոքր շառավղով շրջանը ընկած է մեծ շառավղով շրջանի մեջ:

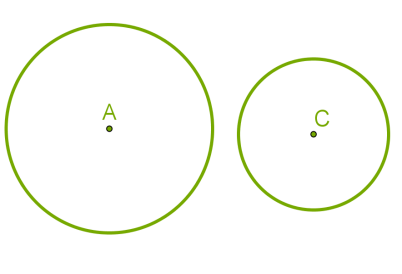
Առաջին տարբերակում կենտրոնների հեռավորությունը մեծ է շառավիղների գումարից:

Երկրորդ տարբերակում կենտրոնների հեռավորությունը փոքր է շառավիղների տարբերությունից:

Առաջադրանքներ․

1)Տրված են երկու շրջանագծեր, որոնք ունեն մեկ ընդհանուր կետ:

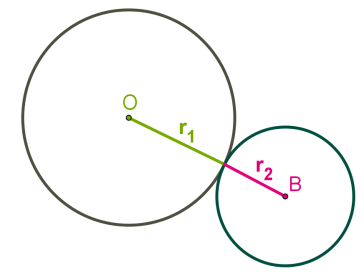
r1-ը և r2-ը համապատասխանաբար մեծ և փոքր շրջանագծերի շառավիղներն են:

Ընտրիր ճիշտ պնդումը:

• OB>r₁+r₂
• r₁+r₂=OB
• r₁+r₂>OB

2)Տրված են հետևյալ երկու շրջանագծերը, որոնք ընդհանուր կետեր չունեն:

r₁-ը և r₂-ը համապատասխանաբար մեծ և փոքր շրջանագծերի շառավիղներն են:

Ընտրիր ճիշտ պնդումը:

• r₁−r₂=AC
• AC<r₁−r₂
• AC=r₁+r₂

3)Գտիր ED-ն, եթե AC= 4 սմ, իսկ շրջանագծերի կենտրոնների միջև հեռավորությունը 5 սմ է: 

5-4=1

4)Գծիր տրված O և B կենտրոններով մեկ ընդհանուր կետ ունեցող շրջանագծեր, որոնց շառավիղները հավասար են՝ r₁=28 սմ և r₂=10 սմ:

Հաշվիր OB հեռավորությունը:

1)Շրջանագծին ներգծած է ABCD քառանկյունը, որի մեջ <A=104^o և <B=71^o։ Գտեք անկյուններ C-ն և D-ն։

<C=180-104=76
<D=180-71=109

2)Արդյոք կարելի՞ է տրված ABCD քառանկյանը արտագծել շրջանագիծ, եթե՝

ա)<A=64^o, <B=95^o, <C=106^o
<A+<C=170
Ոչ

բ)<A=72^o, <B=69^o, <D=111^o
<B+<D=180
Այո

գ)<A=90^o, <C=90^o, <D=80^o
<A+<C=180
Այո

դ)<A=2α, <B=5α^o, <C=7α^o ,<D=4α
2α+5α+7α+4α=360
18α=360
α=20
<A=2•20=40
<B=5•20=100
<C=7•20=140
<D=4•20=80
<A+<C=180
<B+<D=180
Այո

3)

<M=180-53=127
<N=180-75=105

4)Տրված է MK+EF=40: P_MEFK -?

ME+KF=MK+EF
P_MEFK=40+40=80

5)Տրված է NE=MF:  EF+MN -?

<E=30 => EN=2•4=8
EF+MN=EN+MF
EF+MN=8+8=16

Եթե քառանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ քառանկյան ներգծյալ շրջանագիծ:

Ոչ բոլոր քառանկյուններն ունեն ներգծյալ շրջանագիծ, քանի որ՝ չորս անկյունների կիսորդները կարող են նույն կետում չհատվել: 

Եթե քառանկյանը ներգծվել է շրջանագիծ, ապա քառանկյան հանդիպակաց կողմերի գումարները հավասար են՝  a+c=b+d:

Եթե քառանկյան հանդիպակաց կողմերի գումարները հավասար են, ապա այդ քառանկյունն ունի ներգծյալ շրջանագիծ:

Եթե քառանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:

Ոչ բոլոր քառանկյունները ունեն արտագծյալ շրջանագիծ՝ հաճախ քառանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի քառանկյան բոլոր չորս գագաթներով: 

Այս հարցը պարզվում է հետևյալ պնդման միջոցով:

Եթե քառանկյան հանդիպակաց անկյունների գումարը 180° է, ապա նրան կարելի է արտագծել շրջանագիծ:

Առաջադրանքներ․

1)Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերը հավասար են 2սմ և 8սմ։ Գտեք սեղանի պարագիծը։

8+2=10
10+10=20

2)Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերից մեկը հավասար է մյուսի եռապատիկին, իսկ սեղանի սրունքը 8սմ է։ Գտեք սեղանի հիմքերը։

x+3x=8+8
4x=16
x=4

3)Գտեք շրջանագծին արտագծած հավասարասրուն սեղանի կողմերը, եթե նրա պարագիծը 40սմ է, իսկ հիմքերից մեկը 4 անգամ փոքր է մյուսից։

x+4x=y+y
5x=2y
x+4x+y+y=40
5x+2y=40
2y+2y=40
4y=40
y=10
5x=20
x=4
4•4=16

4)Հավասարասրուն սեղանին ներգծած է շրջանագիծ։ Այդ սեղանի պարագիծը 60սմ է։ Գտեք նրա սրունքը։

P=60
a+y=2x
P=a+y+2x
P=4x
60:4=15
x=15

5)Հավասարասրուն սեղանի սրունքը 8սմ է, իսկ փոքր հիմքին առընթեր անկյունների գումարը՝ 300^օ ։ Գտեք այդ սեղանին ներգծած շրջանագծի շառավիղը։

<B+<C=300
2r=8:2=4
r=4:2=2

1)Շրջանագծին ներգծված է ABC եռանկյունն այնպես, որ AB-ն տրամագիծ է։ Գտեք եռանկյան անկյունները, եթե՝

ա) U BC=134⁰

<A=134:2=67
<C=180:2=90
<B=90-67=23

բ)U AC=70⁰ 

<B=70:2=35
<C=180:2=90
<A=90-35=55

2)Շրջանագծին ներգծված է BC հիմքով ABC հավասարասրուն եռանկյունը։ Գտեք եռանկյան անկյունները, եթե U BC=102⁰։

<A=102:2=51
<B=<C=(180-51):2=64,5

3)Ուղղանկյուն եռանկյան ներքնաձիգը 13 սմ է, իսկ էջերի գումարը՝ 17 սմ։ Գտեք եռանկյան ներգծյալ շրջանագծի շառավիղը։

r=(a+b-c):2
(17-13):2=2

4)Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36 սմ։ Գտեք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը։

P=a+b+c
r=(a+b-c):2
a+b+15=36
a+b=21
r=(21-15):2=3

5)ABC եռանկյանը արտագծված է շրջանագիծ։ Գտեք այդ շրջանագծի շառավիղը, եթե AC=24սմ, <A=60⁰, <B=30⁰ ։

<B=30^o, => AB=2AC=48
R=AB/2=24

1.Նշիր եռանկյունները, որոնց արտագծված է շրջանագիծ:

2.Նշիր եռանկյունները, որոնց ներգծված է շրջանագիծ:

3. Եռանկյանը ներգծված է շրջանագիծ: Հաշվիր <COA, <AOB, <COB եթե ∢OMN=32° և ∢ONL=37°

L=42

AOB=106

AOC=116

COL=BOC=180-21-90=69

COB=69+69=138

1)Գծագրերում գտնե՛լ ABC անկյունը․

120

30

130

120

60

2)Գծագրերում գտնել x աղեղը․

135

270

3)Գծագրերում գտնել x անկյունը․

39

23

4)Գտնել անհայտ անկյունները․

53

90

Ըստ գծագրերի տվյալների գտեք անհայտ անկյունը․

1)

30º

2)

130º

3)

65º

4)

90º

5)

120º

6)

60º

1.Որքա՞ն է ներգծյալ անկյունը, որը հենված է 28° աստիճանային չափով աղեղի վրա:

14

2.Դիցուք BAC անկյունը 35° է: Որքա՞ն է BnC աղեղի աստիճանային չափը։

70

3.Գտիր ASB անկյունը, եթե ASB աղեղի աստիճանային չափը 268° է:

360-268=92

92:2=46

4.Գտիր BOC և BAC անկյունները, եթե ∪AB=130° ∪AC=150° ։

360-150-130=80

80:2=40

5.Հաշվիր AOB եռանկյան անկյունները, եթե ∪AB=100°։

AOB=UAB=100

6. ACB աղեղի աստիճանային չափը 260° է: Գտիր AOB և ACB անկյունները:

360-260=100

AOB=100

ACB=100:2=50

1)Ըստ գծագրերի տվյալների՝ գտեք x-ը․

ա)

152+80=232
360-232=128
128:2=64

բ)

125+60=185
360-185=175

գ)

180+112=292
360-292=68
68:2=34

դ)

215+40=255
360-255=105

2)AB կիսաշրջանագծի վրա վերցված են C և D կետերն այնպես, որ

∪AC=57^o, ∪BD=63^o   

Գտեք CD լարը, եթե շրջանագծի շառավիղը 12 սմ է։

180-120=60
Եռ․ CED հավասարակողմ է
Հետևաբար CD=12

3)AOB կենտրոնային անկյունը 30^o -ով մեծ է AB աղեղին հենված ներգծյալ անկյունից։ Գտեք այդ անկյուններից յուրաքանչյուրը։

2x=x+30
x=30

Շրջանագիծ կոչվում է երկրաչափական այն պատկերը, որը կազմված է հարթության բոլոր այն կետերից, որոնք գտնվում են տրված կետից տրված հեռավորության վրա:   

Այդ կետը կոչվում է շրջանագծի կենտրոն, իսկ տրված հեռավորությունը՝ շրջանագծի շառավիղ:

Շառավիղը հատված է, որը միացնում է շրջանագծի կենտրոնը շրջանագծի ցանկացած կետի հետ: Սահմանումից հետևում է, որ կարելի է տանել անվերջ թվով շառավիղներ, և դրանք բոլորը կունենան միևնույն երկարությունը:

Շրջանագծի երկու կետեր միացնող հատվածը կոչվում է լար:

Եթե լարը անցնում է շրջանագծի կենտրոնով, ապա այն կոչվում է շրջանագծի տրամագիծ:

Տրամագիծն ամենաերկար լարն է:

Շրջանագծում կարելի է տանել նաև անվերջ թվով տրամագծեր:

Շրջանագծի ցանկացած երկու կետեր շրջանագիծը տրոհում են երկու մասի, որոնցից յուրաքանչյուրը կոչվում է շրջանագծի աղեղ:

Եթե շրջանագծի վրա նշենք երկու կետ, ապա առաջանում են երկու աղեղներ: Այդ պատճառով աղեղի նշանակման համար օգտագործում են լատիներեն երեք տառ, որոնք կարող են լինել ինչպես մեծատառեր, այնպես էլ՝ փոքրատառեր:  

Վերևի նկարում կարող ենք նշել BDH, ACG և մյուս աղեղները:

Ներքևի նկարում գծված են AxB և AyB աղեղները:

Լարի միջնակետով անցնող շառավիղը

1.Լարի միջնակետով անցնող շառավիղը ուղղահայաց է այդ լարին։

2․Լարը հատող և նրան ուղղահայաց շառավիղն անցնում է այդ լարի միջնակետով։

Առաջադրանքներ․

1)Հաշվիր CA -ն, եթե CD=8 սմ և ∢AOD=120°

2)Տրված են շրջանագիծ և մի քանի հատվածներ: Որո՞նք են դրանցից հանդիսանում շառավիղներ, լարեր և տրամագծեր:

3) Ընտրիր շրջանագծի լարը:

Կարող են լինել մի քանի ճիշտ պատասխաններ:

4) Ո՞ր հատվածներն են հանդիսանում շրջանագծի տրամագիծ:

5) Տրված է՝ MN=7սմ, ∢ONM=60°։Գտիր՝ KN-ը։

6)ABCD զուգահեռագծի B  գագաթից АD կողմին տարված է  BH բարձրությունը, որ AB կողմի հետ կազմում է 40 աստիճանի անկյուն։ Գտեք զուգահեռագծի բոլոր անկյունները։

7)Զուգահեռագծի պարագիծը 100սմ է:Նրա կողմերից մեկը մյուսից մեծ է 10սմ-ով: Գտեք զուգահեռագծի կողմերը: