Category: Երկրաչափություն 8

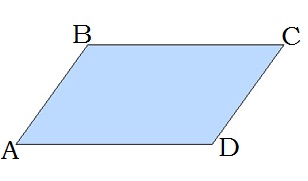
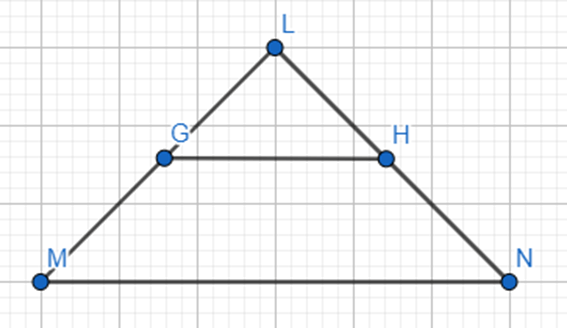
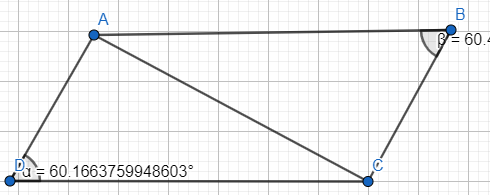
Սեղան է կոչվում այն քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը զուգահեռ չեն:

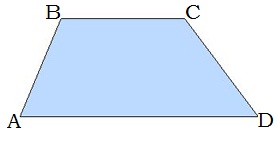
Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր:

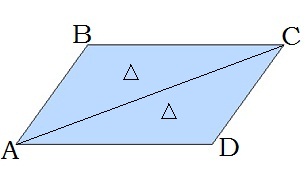
AD -ն և BC -ն սեղանի հիմքերն են:  

Սեղանի կողմերը, որոնք զուգահեռ չեն, կոչվում են սրունքներ:

AB -ն և CD -ն սեղանի սրունքներն են:  

Սեղանի հատկությունները․

Սեղանի ներքին անկյունների գումարը (ցանկացած քառանկյան) 360° է:

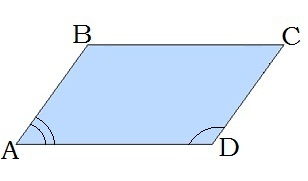
Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:

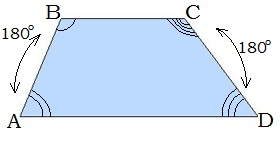
Կան սեղանի մի քանի տեսակներ: Հաճախ դիտարկվում են ուղղանկյուն և հավասարասրուն սեղանները:

Ուղղանկյուն սեղան

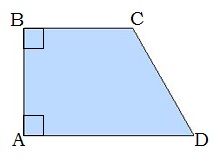
Սեղանը կոչվում է ուղղանկյուն սեղան, եթե նրա սրունքներից որևէ մեկը ուղղահայաց է հիմքերին:

Հավասարասրուն սեղան

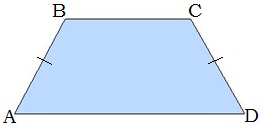
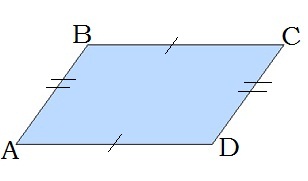
Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան:

Հետևյալ հատկությունները բնորոշ են միայն հավասարասրուն սեղաններին:

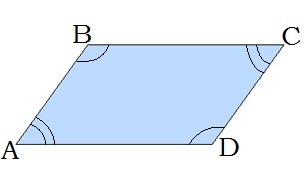
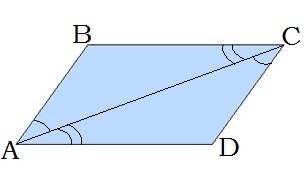
1. Հավասարասրուն սեղանի հիմքերին առընթեր անկյունները զույգ առ զույգ հավասար են:

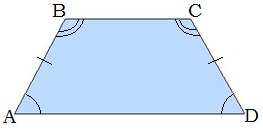
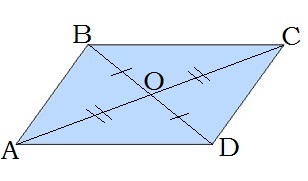
2. Հավասարասրուն սեղանի անկյունագծերը հավասար են:

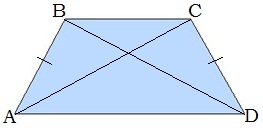
AC=BD

Հավասարասրուն սեղանի հայտանիշները․

1. Եթե սեղանի հիմքին առընթեր անկյունները հավասար են, ապա սեղանը հավասարասրուն է:

2. Եթե սեղանի անկյունագծերը հավասար են, ապա սեղանը հավասարասրուն է:

Սեղանի միջին գիծը․

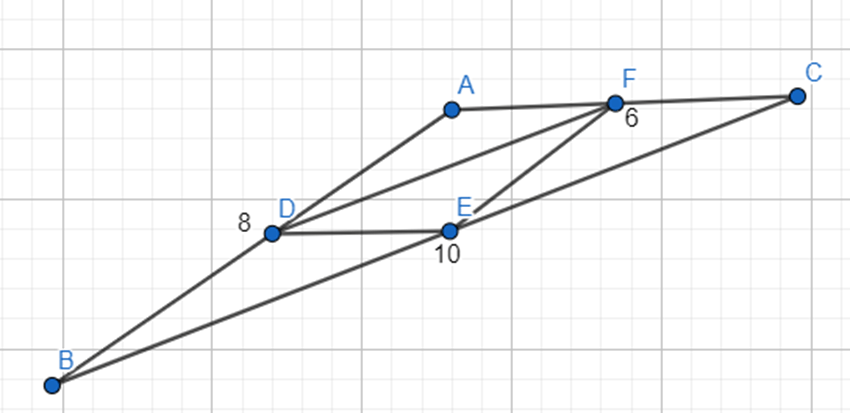
Սեղանի սրունքների միջնակետերը միացնող հատվածը կոչվում է սեղանի միջին գիծ:

Սեղանի միջին գիծը զուգահեռ է հիմքերին և հավասար է նրանց կիսագումարին:

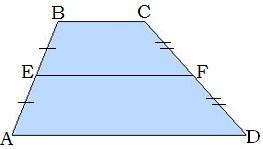
EF∥BC

EF∥AD

EF=(BC+AD)/2

Սեղանն ունի ընդամենը մեկ միջին գիծ:

Առաջադրանքներ․

1) Տրված է՝ ∢A=37°∢C=121° : Գտիր՝ ∢B,∢D-ն։

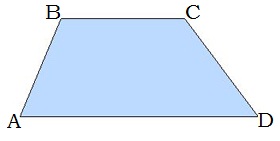
180-37=143

180-121=59

2)Հաշվիր ABCD սեղանի անկյունները, եթե ∢A=30°:

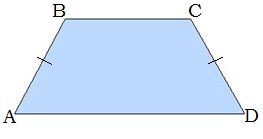
D=A=30

180-30=150

B=C=150

3) Տրված է՝ AE=EB, CF=FD, BC=28 մ, AD=30 մ: Գտիր՝ EF-ը:

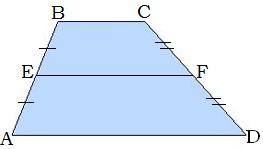
30+28=58

58:2=29

4)Սեղանի հիմքերի հարաբերությունը հավասար է 2:7: Հաշվիր սեղանի մեծ հիմքը, եթե նրա փոքր հիմքը հավասար է 12 սմ -ի:

12։2=6
6*7=42
Լրացուցիչ աշխատանք (տանը)․

1) Նշիր ճիշտ պնդումը՝

ա)Հավասարասրուն սեղանի սրունքները զուգահեռ են:

բ)Ուղղանկյուն սեղանի հիմքերը հավասար են:

գ)Ցանկացած սեղանի հիմքերը զուգահեռ են:

2)Սեղան կոչվում է այն քառանկյունը, որի

ա)կողմերը զույգ առ զույգ զուգահեռ են:

բ)երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը՝ ոչ:

3) Սեղանը կոչվում է հավասարասրուն, եթե

ա)նրա սրունքները հավասար են:

բ)նրա սրունքները զուգահեռ են:

Տեսական մասը կրկնեք այստեղ․

Առաջադրանքներ․

1)Զուգահեռագծի պարագիծը 48սմ է։ Գտեք զուգահեռագծի կողմերը, եթե՝

ա) կողմերից մեկը մյուսից մեծ է 3 սմ-ով,

x+x+3+x+x+3=48
4x+6=48
4x=48-6
4x=42
x=42/4
x=10,5
10,5+3=13,5

բ) կողմերից մեկը երկու անգամ մեծ է մյուսից:

x+2x+x+2x=48
6x=48
x=48/6
x=8
8×2=16

գ)կողմերից մեկը երկու անգամ մեծ է մյուսից
1+3=4
48:4=12 (1)
12*3=36 (3)

2)Ըստ գծագրի տվյալների՝ գտե՛ք զուգահեռագծի պարագիծը.

3x+5=6x-10

x=20

DA=15

15+15+20+20=70

3)ABCD զուգահեռագծի պարագիծը 50 սմ է, <C=30⁰, իսկ CD ուղղին տարված BH ուղղահայացը 6,5 սմ է։ Գտեք զուգահեռագծի կողմերը։

Լրացուցիչ աշխատանք (տանը).

1)Գտե՛ք ABCD զուգահեռագծի անկյունները, եթե՝

ա) ∠ A = 45°
45×2=90

180-90=90

90:2=45

բ) ∠ C – ∠ D = 50°

գ) ∠ A + ∠ C = 81°
180-81=99

99:2=49,5

դ) ∠ A = 0,5∠ B։

2)Ըստ գծագրի տվյալների՝ գտե՛ք զուգահեռագծի պարագիծը.

3)Զուգահեռագծի կիսապարագիծը 24 սմ է, կողմերից մեկը երկու անգամ մեծ է մյուսից, իսկ մեծ կողմին տարված բարձրությունը 4 սմ է։ Գտե՛ք զուգահեռագծի անկյունները։

Զուգահեռագիծ կոչվում է այն քառանկյունը, որի հանդիպակաց կողմերը զույգ առ զույգ զուգահեռ են:

Զուգահեռագծի հատկությունները.

1. Զուգահեռագծի հանդիպակաց կողմերը հավասար են՝ AB=DC,BC=AD

2. Զուգահեռագծի հանդիպակաց անկյունները հավասար են՝ ∢A=∢C,∢B=∢D

3. Զուգահեռագծի անկյունագծերը հատման կետով կիսվում են՝ BO=OD, AO=OC

4. Զուգահեռագիծը անկյունագծով բաժանվում է երկու հավասար եռանկյունների՝ ABC և CDA եռանկյունները հավասար են:

5. Զուգահեռագծի յուրաքանչյուր կողմին առընթեր անկյունների գումարը 180 աստիճան է՝ ∢A+∢D=180°

6. Անկյունագծի խաչադիր անկյունները հավասար են՝ ∢BAC=∢ACD, ∢BCA=∢CAD

Զուգահեռագծի հայտանիշները.

Զուգահեռագծի հայտանիշները թույլ են տալիս պարզելու, թե արդյո՞ք տրված քառանկյունը զուգահեռագիծ է:

1. Եթե քառանկյան երկու կողմերը հավասար են և զուգահեռ, ապա քառանկյունը զուգահեռագիծ է: 

2. Եթե քառանկյան հանդիպակաց կողմերը զույգ առ զույգ հավասար են, ապա քառանկյունը զուգահեռագիծ է: 

3. Եթե քառանկյան անկյունագծերը հատվում և հատման կետով կիսվում են, ապա քառանկյունը զուգահեռագիծ է:

Առաջադրանքներ․

1)

P=6+6+10+10=32

2)

3)

AB = 15

AD = 30

Լրացուցիչ աշխատանք (տանը).

1)

Հիմա բացատրեմ ինչու ՝ եթե A-ն 40 աստիճան է ապա C-ն էլ, քանի որ զուգահեռագծի հանդիպակաց անկյունները հավասար են՝ ∢A=∢C,∢B=∢D, իսկ B-ն հավասար է 140 , քանի որ զուգահեռագծի յուրաքանչյուր կողմին առընթեր անկյունների գումարը 180 աստիճան է՝ ∢A+∢B=180° իսկ 180 — 40 = 140, իսկ եթե B-ն 140 է ապա D-ն էլ է 140

2)

A անկյունը՝ 60

B անկյունը՝ 120

3)

BO = 6

OC = 8,5

Առաջադրանքներ․

1)RS -ը ABC եռանկյան միջին գիծն է՝ R∈AB, S∈AC: Ընտրիր ճիշտ տարբերակը`

ա)RS∥BC

բ)RS⊥AB

գ)երկուսն էլ ճիշտ են

2)KLM եռանկյան մեջ տարված է GH միջին գիծը, ընդ որում՝ G∈KL, H∈KM: GH միջին գծի վերաբերյալ, ո՞ր պնդումն է ճիշտ: Ընտրիր ճիշտ պատասխանը:

ա)GH∥LM

բ)GH⊥LM

գ)երկուսն էլ ճիշտ են

3)

DF=BC/2=5
FE=AB/2=4
DE=AC/2=3
P=5+4+3=12

Լրացուցիչ աշխատանք (տանը).

1)LMN եռանկյան մեջ GH-ը միջին գիծ է՝ G∈LM, H∈LN: Միջին գծի  վերաբերյալ, ո՞ր պնդումն է ճիշտ: Ընտրիր ճիշտ պատասխանը:

ա)GH=MN/2

բ)GH=2MN

գ)երկուսն էլ ճիշտ են

2)

FG=BE/2=8
GH=AD/2=6
IH=BE/2=8
FI=AD/2=6

Տեսական մասը կրկնեք այստեղ․

Առաջադրանքներ․

1)

1)180(n-2)/n=Ուռուցիկ բազմ․ միանկյունը
ա)180(n-2)/n=90
2(n-2)=n
2n-4=n
n=4
բ)180(n-2)/n=60
180(n-a)=60
3(n-2)=n
3n-n=6
2n=6
n=3
Նույն ձեւով ՝ գ, 6 դ, 5

2)

Պատ. 75

3)

1. 23
2. 50
3. 57
4. 70

Լրացուցիչ աշխատանք (տանը).

1)

1) 2x+3x+4x+5x+6x=540
20x=540
x=27
հետ․՝ 2*27=54
3*27=81
4*27=108
5*27=135
6*27=162

2)

Պատ.՝ 23,20,19,18

1)Քառանկյան կողմերը հարաբերում են, ինչպես 3:4:5:7: Գտե՛ք քառանկյան կողմերը, եթե պարագիծը 380սմ է։

3+4+5+7=19

380:19=20

ab=20×3=60

bc=20×4=80

cd=20×5=100

da=20×7=140

2)ABCD ուռուցիկ քառանկյունում <A = 20o , <B = 90o, իսկ C անկյունը 30օ-ով մեծ է D անկյունից։ Գտե՛ք <C-ն և <D-ն։

360-90-20=250

250:2=125

∠d=125-30=95

∠c=125+30=155

3)Քանի՞ կողմ ունի ուռուցիկ բազմանկյունը, եթե նրա անկյունների գումարը 540o է։

540:180=3

4)Գտե’ք ուռուցիկ քառանկյան անկյունները, եթե դրանցից մեկը մյուսներից մեծ է համապատասխանաբար 10o-ով, 20o-ով , 30o-ով։

5)Գտե’ք ուռուցիկ հնգանկյան անկյունները, եթե դրանք համեմատական են 5, 6, 4, 6, 6 թվերին։

Լրացուցիչ աշխատանք (տանը).

1)Գտե՛ք ABCD քառանկյան պարագիծը, եթե AB=12սմ, BC=21սմ, CD=14սմ, AD=15սմ։

12+21+14+15=62

2)Հնգանկյան կողմերը հարաբերում են, ինչպես 2:3:5:7:8: Գտե՛ք հնգանկյան պարագիծը, եթե դրա ամենամեծ կողմը 16սմ է։

16:8=2

2×2=4

2×3=6

2×5=10

2×7=14

16+14+10+6+4=50

3)Գտե՛ք ուռուցիկ քառանկյան անկյունները, եթե դրանք համեմատական են 1, 2, 4, 5 թվերին։

1.Հավասարասրուն եռանկյան պարագիծը հավասար է 1մ-ի, իսկ հիմքը՝ 0,4 մ-ի: Գտեք սրունքի երկարությունը։

1-04=0,6

0,6:2÷0,3

2.Հավասարասրուն եռանկյան արտաքին անկյուններից մեկի մեծությունը 120o է։ Գտեք այդ եռանկյան անկյունների մեծությունները։

180-120=60

60×2=120

180-120=60

եռանկյունը նաև հավասարակողմ է

3.<3-ը երկու անգամ մեծ է <1 -ից : Գտնել <2-ը և <4-ը։

<3=120°, <1=60°

<3=<2 խաչադիր անկյուններ

<1=<4 խաչադիր անկյուններ

Քանի որ <3-ը երկու անգամ մեծ է <1 -ից <1=60, <2=120, <3=120, <4=60

1. Տեղեկատվական հետազոտություն
   Մեծ մաթեմատիկոսների մասին հակիրճ տեղեկատվության օրինակ.

Պյութագորաս (մոտ 570–495 մ.թ.ա.)

Հիմնական ձեռքբերումները. Պյութագորասի թեորեմ երկրաչափության մեջ (եռանկյունու մեջ ոտքերը և հիպոթենուսը կապված են հավասարման միջոցով
𝑎2+𝑏2𝑐2𝑎2+b2= c2)
Հետաքրքիր փաստեր. Պյութագորասը նաև հիմնեց փիլիսոփայական դպրոց և ուսումնասիրեց թվերն ու դրանց հատկությունները:
Կարլ Ֆրիդրիխ Գաուս (1777–1855)

Հիմնական ձեռքբերումները՝ թվերի տեսություն, նվազագույն քառակուսիների մեթոդ, վիճակագրության հիմք։
Հետաքրքիր փաստեր.
Անդրեյ Ռամանուժան (1887–1920)

Հիմնական ձեռքբերումները՝ Ռամանուջանի թեորեմ, հետազոտություն թվերի և անվերջ շարքերի անալիտիկ տեսության մեջ։
Հետաքրքիր փաստեր. Ռամանուջանն ինքն է մշակել արդյունքներից շատերը, և նրա աշխատանքի մեծ մասը զարմանալիորեն ճշգրիտ և բարդ էր:

2. Հարցեր, հարցերի օրինակներ.

Ո՞վ է Պյութագորասը և ո՞րն է նրա ամենահայտնի հայտնագործությունը:
Որո՞նք էին Կարլ Ֆրիդրիխ Գաուսի հիմնական ձեռքբերումները մաթեմատիկայի բնագավառում:
Ի՞նչ նշանակություն ունի Ռամանջանի աշխատանքը ժամանակակից մաթեմատիկայի մեջ։

3. Պյութագորասը և նրա ներդրումը մաթեմատիկայի մեջ:

Տեքստ՝ Պյութագորասը հին հույն մաթեմատիկոս և փիլիսոփա էր, ով նշանակալի ներդրում ունեցավ մաթեմատիկայի զարգացման գործում։ Նրա թեորեմը, որը հայտնի է որպես Պյութագորասի թեորեմ, նկարագրում է ուղղանկյուն եռանկյան կարևոր հատկությունը։ Այն նշում է, որ ցանկացած ուղղանկյուն եռանկյունում հիպոթենուսի երկարության քառակուսին հավասար է ոտքերի երկարությունների քառակուսիների գումարին։ Այս հայտնագործությունը մեծ նշանակություն ունի և կիրառվում է գիտության և ճարտարագիտության տարբեր ոլորտներում։

4. Տեսանյութի սցենար
   Օրինակ սցենար.

Ներածություն: Բարև: Այսօր մենք կխոսենք մեծ մաթեմատիկոս Պյութագորասի և նրա կարևոր թեորեմի մասին։

Հիմնական մասը՝ Պյութագորասը ապրել է Հին Հունաստանում և հայտնի է եղել երկրաչափական ուսումնասիրություններով։ Նրա թեորեմը, որը նկարագրում է ուղղանկյուն եռանկյան կողմերի հարաբերությունները, մինչ օրս ակտիվորեն օգտագործվում է մաթեմատիկայում։

Եզրակացություն. Մենք տեսնում ենք, թե որքան կարևոր են Պյութագորասի հայտնագործությունները և ինչպես են դրանք շարունակում ազդել մեր կյանքի վրա: Հուսով եմ, որ ձեզ դուր եկավ ավելին իմանալ նրա մասին: