Category: Հանրահաշիվ 9

1)Գտե՛ք նշված քառակուսային եռանդամի գրաֆիկի գագաթի կոորդինատները.
ա) y = x² — 5x + 3

գ) y = 2x² — 4x + 6

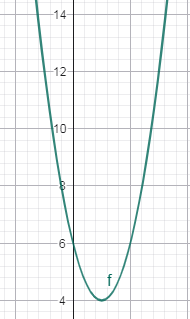
դ) y = — 6x² — 18x + 24

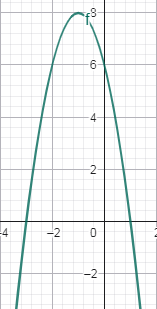
3)Քառակուսային եռանդամի գրաֆիկի գագաթի կոորդինատներն են (x₀, y₀), իսկ զրոները՝ x₁-ն ու x₂-ը: Գտե՛ք x₀-ն, եթե հայտնի է, որ. ա) x₁ = 4, x₂ = 10 բ) x₁ = — 5, x₂ = — 9

(-5+-9)/2=-7 գ) x₁ = — 3, x₂ = 9

(-3+9)/2=3 դ) x₁ = — 6, x₂ = 0

(-6+0)/2=-3 ԼՈՒԾՈՒՄ` ա) f(x) = ax² + bx + c պարաբոլի համար x₀ = −b/2a: Ըստ Վիետի թեորեմի՝ x₁ + x₂ = −b/a: Այս հավասարության երկու կողմը բաժանելով 2-ի՝ ստանում ենք (x₁ + x₂)/2 = −b/2a, որը հենց x₀-ն է: Քանի որ x₁ = 4 և x₂ = 10, ուրեմն՝ x₀ = (4 + 10)/2 = 7:

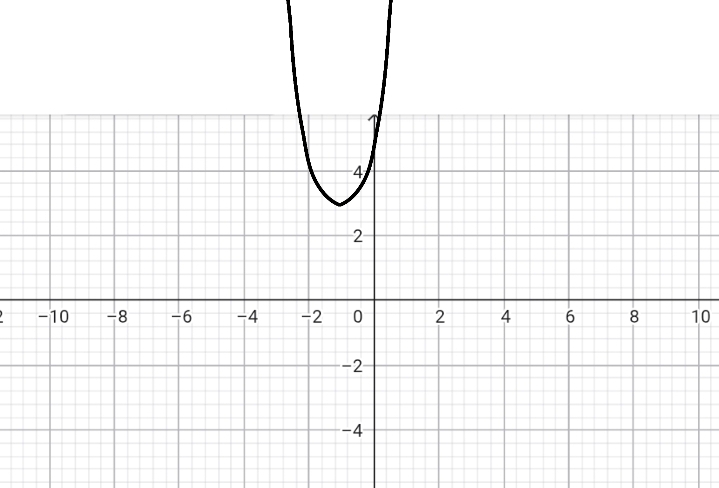
4)Գծե՛ք քառակուսային եռանդամի գրաֆիկը: Գտե՛ք այդ գրաֆիկի գագաթն ու զրոները. ա) x² + 4x — 5

(-2;-9)

(-5;0)

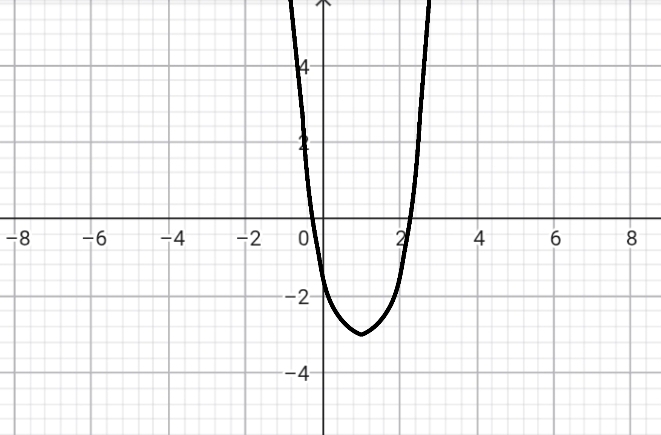
(1;0) բ) x² — 6x + 5

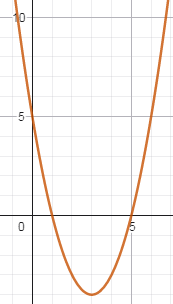
(3;-4)

(1;0)

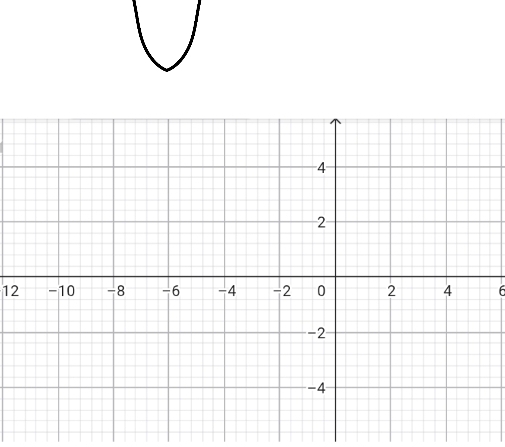
(5;0) գ) 5x² — 15x + 10

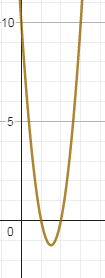
(1.5;-1.25)

(1;0)

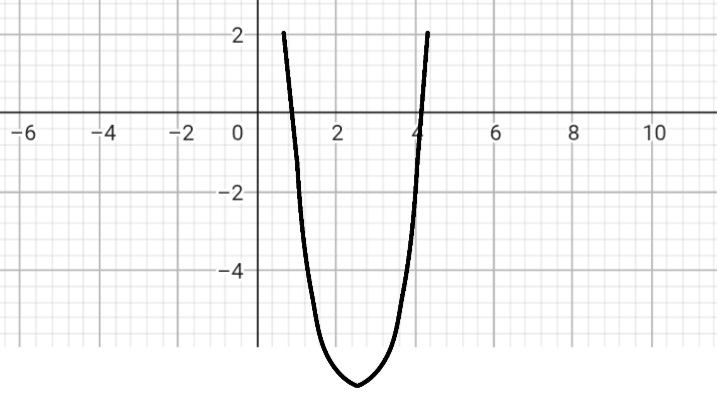
(2;0) դ) 4x² — 9x + 10

(1.125;≈4.9) ե) — 2x² + 8x — 6

(2;2) (1;0)

(3;0)

զ) — 3x² + 8x — 6

(-4/3;-34/3)

1)Հաշվել արտահայտության արժեքը․

ա)1 4/7
բ)29/39
գ)-1/20
դ)12/75 4/25

2)Հաշվել արտահայտության արժեքը․

ա)|5a + 2| — |a — 2|, եթե a = 4
22-2=20

բ)|3a — 6| — |2a — 1|, եթե a = -2
12-5=7

գ)|2a — 5| — |5a — 3|, եթե a = -6
17-33=-16

դ)|4a + 2| — |a|, եթե a = -2
6-2=4

3)Հաշվել արտահայտության արժեքը․

ա)8
բ)25
գ)5
դ)25

4)Լուծել խնդիրները․

1)8 տրակտոր 10 օրում վարում են 320 հա տարածք։

ա)3 տրակտորները 5 օրում քանի՞ հա տարածք կվարեն։
60

բ)8 տրակտորները քանի՞ օրում կվարեն 160 հա տարածք։
5

2)4 տրակտոր 7 օրում վարում են 280 հա տարածք։

ա)3 տրակտորները 4 օրում քանի՞ հա տարածք կվարեն։
120

բ)5 տրակտորները քանի՞ օրում կվարեն 300 հա տարածք։
6

3)5 տրակտոր 7 օրում վարում են 210 հա տարածք։

ա)2 տրակտորները 3 օրում քանի՞ հա տարածք կվարեն։
36

բ)4 տրակտորները քանի՞ օրում կվարեն 120 հա տարածք։
5

1)Տրված է y = x2 ֆունկցիայի գրաֆիկը: Այն y-ների առանցքի երկայնքով ձգեցին a անգամ, այնուհետև տեղաշարժեցին b միավորով ձախ և c միավորով ներքև։ Արդյունքում ստացվեց y = 5 * (x + 4)2 — 2 ֆունկցիայի գրաֆիկը: Գտե՛ք a-ն, b-ն ու c-ն:

a=5 b=4 c=2

2)Տրված է y = — x2 ֆունկցիայի գրաֆիկը: Այն y-ների առանցքի երկայնքով ձգեցին 3 անգամ, այնուհետև 5 միավորով աջ և 7 միավորով վերև։ Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց:

y=3*(x-5)+7

3)Տրված է y = x2 ֆունկցիայի գրաֆիկը։ Այն սեղմեցին a անգամ, այնուհետև տեղաշարժեցին 4 միավորով ներքև։ Արդյունքում ստացվեց y = 1/8 * x2 — 4 ֆունկցիայի գրաֆիկը: Գտե՛ք a-ն:

8

4)Պատկերե՛ք ֆունկցիայի գրաֆիկը.

ա) y = (x + 1)2 + 3

բ) y = 3 * (x — 2)2 — 1 ,

գ) y = — 2 * (x + 7)2 + 1

5)Գտե՛ք հետևյալ պարաբոլի գագաթի կոորդինատները.

ա) y = 2(x — 4)2

4;0

բ) y = — (x + 2)2 — 5

-2;-5

գ) y = x2 + 5

0;5

դ) y = 8 * (x — 11)2 + 20

11;20

ե) y = — 5/9 * (x + 3)2 + 1

-3;1

զ) y = 4 * (x — 3)2 — 12

3;-12

1)Գծե՛ք f(x) = x² պարաբոլը: Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե f(x)-ի գրաֆիկը տեղափոխենք ա) 2 միավորով աջ, բ) 5 միավորով ձախ:

f(x)=(x-2)²

f(x)=(x+5)²

2)Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե f(x) = 3x² ֆունկցիայի գրաֆիկը տեղափոխենք ա) 4 միավորով ձախ, բ) 1 միավորով աջ:

f(x)=3*(x+4)²

f(x)=3*(x-1)²

3)Գծե՛ք f(x) = 4x² ֆունկցիայի գրաֆիկը: Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե այն տեղափոխենք ա) 7 միավորով ձախ, բ) 3 միավորով աջ:

f(x)=4*(x+7)²

f(x)=4*(x-3)²

4)Հայտնի է, որ f(x) ֆունկցիայի գրաֆիկը տեղաշարժելով ա) 5 միավորով աջ, բ)12 միավորով ձախ՝ ստացվել է y = x² պարաբոլը: Գտե՛ք f(x) ֆունկցիայի բանաձևը:

f(x)=(x+5)²

f(x)=(x-12)²

5)Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե f(x) = x² պարաբոլը տեղափոխենք.
ա) 2 միավորով աջ և 4 միավորով ներքև,

f(x)=(x-2)²-4

բ) 5 միավորով ձախ և 1 միավորով վերև,

f(x)=(x+5)²+1
գ) 2 միավորով ներքև և 1 միավորով աջ,

f(x)=(x-1)²-2
դ) 3 միավորով ձախ և 5 միավորով ներքև։

f(x)=(x+3)²-5

6)Պատկերե՛ք ֆունկցիայի գրաֆիկը.
ա) y = (x + 4)²

բ) y = (x — 1)² — 3

գ) y = (x + 6)² + 8

դ) y = (x — 4)² + 7

ե) y = (x — 2.5)² — 6.25

զ) y = (x — 4/5)² + 1

1)Հաշվել արտահայտության արժեքը․

16/7

7/5

4

6

23/24

1/5

2)Հաշվել արտահայտության արժեքը․

|-7| + |2| — |-3-2| =4

|-2| + |2| — |1-5| =0

|4a-3| — |2a-2|=5 , եթե a = -2

|2a-4| + |a+3|=8 , եթե a = -1

3)Հաշվել արտահայտության արժեքը․

27

27

4

4

4)Լուծել խնդիրները․

ա)Բադերը և խոզերը միասին ունեն 17 գլուխ և 44 ոտք։

Որքա՞ն բադ կա։

12

Որքա՞ն խոզ կա։

5

բ)Բադերը և խոզերը միասին ունեն 22 գլուխ և 58 ոտք։

Որքա՞ն բադ կա։

15

Որքա՞ն խոզ կա։

7

գ)Բադերը և խոզերը միասին ունեն 22 գլուխ և 56 ոտք։

Որքա՞ն բադ կա։

16

Որքա՞ն խոզ կա։

6

1)Տրված x-երի համար գտե՛ք y-ի այնպիսի արժեք, որ (x, y) կետը լինի y = x² պարաբոլի վրա.
ա) x = 0

0
բ) x = 3

9
գ) x = — 3.2

10.24
դ) x = 111

12321
ե) x = √5.5

5.5

զ) x = — √13

13
է) x = 2√3

12
ը) x = — 6√1.5

9

ա) y = 0

0
բ) y = 25

5
գ) y = 196

14
դ) y = 2.89

1.7
ե) y = — 16

լուծում չունի

զ) y = -2

լուծում չունի
է) y = 2

±√2
ը) y = 45

±√45

3)Ո՞ր կետերում է տրված ուղիղը հատում y = x² ֆունկցիայի գրաֆիկը.
ա) y = 0

(0;0)
բ) y = 5

(±√5;5)
գ) y = — 1.1

չկա
դ) y = 64

(±8;64)

4)Կառուցե՛ք y = x² ֆունկցիայի գրաֆիկի համաչափը x-երի առանցքի նկատմամբ:

5)Տրված է y = x² ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 9, բ) 0, գ) 15, դ)– 25 արժեքը:

(3;9)

(0;0)

(±√15;15)

1)y=f(x−166) ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y=f(x) ֆունկցիայի գրաֆիկը տեղաշարժել 166 միավորով դեպի՝

• վերև
• ձախ
• աջ
• ներքև

2)Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե y = 6x¹⁷ ֆունկցիայի գրաֆիկը Ox առանցքի ուղղությամբ տեղաշարժել 16 միավորով դեպի ձախ:

y=6(x+16)^17

3)y=1/2(x−198)¹³ + 62 ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y = 1/2x¹³ ֆունկցիայի  գրաֆիկը տեղաշարժել 198 միավորով

• x-երի առանցքի ուղղությամբ դեպի ձախ
• x-երի առանցքի ուղղությամբ դեպի աջ
• y-երի առանցքի ուղղությամբ դեպի վերև
• y-երի առանցքի ուղղությամբ դեպի ներքև

և  62 միավորով

ա)x-երի առանցքի ուղղությամբ դեպի աջ

բ)y-երի առանցքի ուղղությամբ դեպի ներքև

գ)x-երի առանցքի ուղղությամբ դեպի ձախ

դ)y-երի առանցքի ուղղությամբ դեպի վերև

4)Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե  y=10x³ ֆունկցիայի գրաֆիկը Oy առանցքի ուղղությամբ 8 միավորով տեղաշարժվի դեպի վերև:

y=10(x)^3+8

5)Նկարում պատկերված է f(x) ֆունկցիայի գրաֆիկը։ Գծե՛ք f(x — a) ֆունկցիայի գրաֆիկը.
ա)a = 3
բ)a = 2
գ)a = — 1
դ)a = 3
ե)a = — 2
զ)a = 4
է)a = -3
ը)a = -2

6)Նկարում պատկերված է f(x — 2) ֆունկցիայի գրաֆիկը: Գծե՛ք f(x) ֆունկցիայի գրաֆիկը.

7)Գտնել A ∩ B բազմությունը, եթե A = {0; 3; 4; 6}, B = {3; 6; 9}։

{3;6}

8)Գտնել A ∩ B բազմությունը, եթե A = {1; 3; 6; 9}, B = {5; 6; 8}։

{6}

9)Գտնել A U B բազմությունը, եթե A = {0; 1; 2; 4}, B = {1; 2; 5}։

{0;1;2;4;5}

10)Գտնել A U B բազմությունը, եթե A = {0; 3; 6; 9}, B = {0; 3; 8}։

{0;3;6;8;9}

11)Գտնել A U B բազմությունը, եթե A = {7}, B = {4; 6}։

{4;6;7}

1)Գտնել 5 հայտարարով բոլոր կանոնավոր կոտորակների գումարը։

2

2)Գտնել 4 հայտարարով բոլոր կանոնավոր կոտորակների գումարը։

3/2

3)Գտնել 6 հայտարարով բոլոր կանոնավոր կոտորակների գումարը։

5/2

4)70-ը բաժանել 2:3 հարաբերությամբ։

28 42

5)60-ը բաժանել 1:4 հարաբերությամբ։

15 45

6)49-ը բաժանել 2:5 հարաբերությամբ։

14 35

7)Հաշվել արտահայտության արժեքը․

5/3-7/2-13/6=-24/6=-4

10/3-3/2-7/6=20-9=4/6=2/3

58/7+33/8-51/7=464+231-408/56=287/56=41/8

125/12+85/13-113/12=1625+1020-1469/156=1176/156=98/13

8)|-4| : |-2| + |-6| * 2 =14

9)6 : |-3| — 2 : |-2| + 1 =2

10)|-2| + |3| — |-4+1| =2

11)Որդին տասը տարեկան է։ Հինգ տարի առաջ նա 7 անգամ փոքր էր հորից։

ա)Քանի՞ տարեկան է հայրը։

40

բ)Քանի՞ տարի հետո հայրը որդուց մեծ կլինի 2 անգամ։

20

12)Որդին ութ տարեկան է։ Երկու տարի առաջ նա 5 անգամ փոքր էր հորից։

ա)Քանի՞ տարեկան է հայրը։

32

բ)Քանի՞ տարի հետո հայրը որդուց մեծ կլինի 3 անգամ։

4

1)Տրված f(x) ֆունկցիայի զրոները 3-ն ու 8-ն են: Գտե՛ք ա) −10f(x), բ) — 4f(x + 1) գ) -2/3 f(x – 4) ֆունկցիայի զրոները:

ա (3;8)

բ (2;7)

գ(7;12)

2)Տրված f(x) ֆունկցիան y-ների առանցքի երկայնքով ձգեցին 1.5 անգամ և իջեցրին 5 միավորով ներքև: Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց:

1,5f(x)-5

3)Տրված է f(x) ֆունկցիան, որի արժեքների տիրույթը [0, 9] միջակայքն է։ Գտե՛ք ա) 4f(x), բ)5/6f(x) ֆունկցիայի արժեքների տիրույթը:

[0;36]

[0;7,5]

4)Տրված է f(x) ֆունկցիայի գրաֆիկը: Պատկերե՛ք 3f(x) ֆունկցիայի գրաֆիկը.

5)Տրված է f(x) ֆունկցիայի գրաֆիկը: Պատկերե՛ք — f(x) ֆունկցիայի գրաֆիկը:

6)Գտնել 3/4 և 5/8 թվերի գումարի հակադարձ թիվը։

8/11

7)Գտնել 2/3 և 3/4 թվերի գումարի հակադարձ թիվը։

12/17

8)Գտնել 4/5 և 1/4 թվերի գումարի հակադարձ թիվը։

21/20

Ենթադրենք՝ վեկտորների գումարը կազմված է մի քանի հավասար վեկտորներից, օրինակ՝ a + a + a: Բնական է, ինչպես և թվերի դեպքում է, այդ գումարը նշանակել 3a – ով: Պարզ է, որ 3a վեկտորը համուղղված է a վեկտորին, իսկ դրա երկարությունը երեք անգամ մեծ է a վեկտորի երկարությունից:
Նկատենք նաև, որ -a + (-a) վեկտորը մի վեկտոր է, որի երկարությունը 2 անգամ մեծ է a վեկտորի երկարությունից և հակուղղված է a վեկտորին:
Այս օրինակները հուշում են, թե ինչպես սահմանենք թվի և վեկտորի արտադրյալը:
Ոչ զրոյական a վեկտորի և k թվի արտադրյալ կոչվում է այն b վեկտորը, որի երկարությունը հավասար է |k|*|a|, ընդ որում՝ a և b վեկտորները համուղղված են, եթե k >= 0 , և հակուղղված են, եթե k < 0 :
a վեկտորի և k թվի արտադրյալը նշանակվում է ka: Նկարում պատկերված են a, 1,5a, – 2a վեկտորները:

Թվի և վեկտորի արտադրյալի սահմանումից հետևում է, որ.
1) Զրոյական վեկտորի և ցանկացած թվի արտադրյալը, ինչպես նաև ցանկացած վեկտորի և զրոյի արտադրյալը զրոյական վեկտոր է. k*0 = 0
0 * a = 0 :
2)a և ka վեկտորները համագիծ են։

Ցանկացած k, m թվերի և ցանկացած a, b վեկտորների համար տեղի ունեն հետևյալ հավասարությունները.
1) (km) a = k(ma) (զուգորդական օրենք),
2) (k+m) a = ka + ma (առաջին բաշխական օրենք),
3) k (a + b) = ka + kb (երկրորդ բաշխական օրենք):

Առաջադրանքներ․

1)Տրված են a և b վեկտորները: Կառուցե՛ք հետևյալ վեկտորները.

ա) 2a
բ) — 2a
գ) 1/3a
դ) 3b
ե)-1/2b
զ) -4b

2)Պարզեցրեք արտահայտությունները.
ա) 3(a + b) — 2(a — b )
բ) 4a + 5b — 2(a + 2b )
գ) 1/3(a + b) + 2/3(a — b)

3)Համուղղված են, թե՞ հակուղղված a և b ոչ զրոյական վեկտորները, եթե.
ա) b = 2a
բ) b = -3a
գ) a = 1/3b
դ)a = -1/2b

4)Գտե՛ք b վեկտորի մոդուլը, եթե |a| = 6 սմ.
ա) b = 4a
բ) b = -3a
գ)b = 1/3a

5)O-ն ABCD զուգահեռագծի անկյունագծերի հատման կետն է: Գտե՛ք k-ն, եթե DA + DC = k · DO:
6)O-ն ABCD զուգահեռագծի անկյունագծերի հատման կետն է: Գտե՛ք k-ն, եթե AB + AD = k · CO։